- Looker
- Looker Forums
- Exploring & Curating Data
- Tutorial: How to do a 2 X 2 Contingency Chi-Square...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
This is a quick tutorial on how to do a 2x2 Contingency Chi-Square using table calcs in Looker. This comes from a question that was asked by Adrian Palacios on the Locally Optimistic community. We couldn’t find relevant examples anywhere and since it was not as straightforward as we anticipated, I thought I’d post this here for the benefit of everyone.
What’s a 2x2 Contingency Chi-Square?
The 2x2 Contingency Chi-Square is used for the comparison of two groups with a dichotomous dependent variable. For those who need a refresher on the theory, you can checkout this PDF from the Portland State University. I’ve used the example from in it as a base for this tutorial.
We know for this example data set that Chisq = 13.649, df = 1, p-value = 0.000, so let’s work to get these values from Looker!
The test data
I created a simple derived table to generate the test data:
view: chi_square_example_dt {
derived_table: {
sql:
select 'party affiliated' as category, 'Trump' as candidate, 383 as support
union all
select 'party affiliated' as category, 'Warren' as candidate, 385 as support
union all
select 'independent' as category, 'Trump' as candidate, 225 as support
union all
select 'independent' as category, 'Warren' as candidate, 342 as support
;;
}
dimension: category {
type: string
sql: ${TABLE}.category ;;
}
dimension: candidate {
type: string
sql: ${TABLE}.candidate ;;
}
dimension: support {
type: number
sql: ${TABLE}.support ;;
}
measure: total_support {
type: sum
sql: ${support} ;;
}
}
Building the query
Step 1: Get our data in a 2x2 table
I’ve selected my first dimension (Category), pivoted my second dimension (Candidate) and added my Total Support measure. I’ve also checked the Totals and Row Totals checkboxes. The result is this:
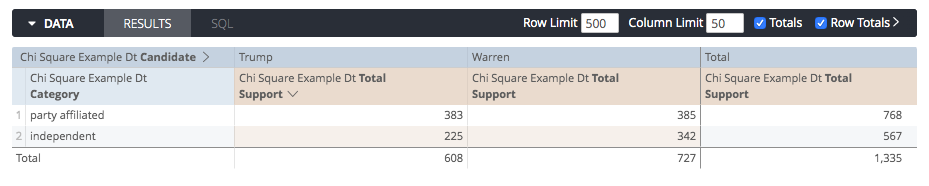
Step 2: Estimate the expected frequency
Now that we have our actuals, we need to calculate their expected frequency which, for any cell, is estimated as (row total * column total) / grand total.
We’ll create a first table calc named Expected Frequency with a Decimals (2) format and the following expression:
(${chi_square_example_dt.total_support:row_total} * ${chi_square_example_dt.total_support:total})
/
sum(pivot_row(${chi_square_example_dt.total_support:total}))
We now get this output:
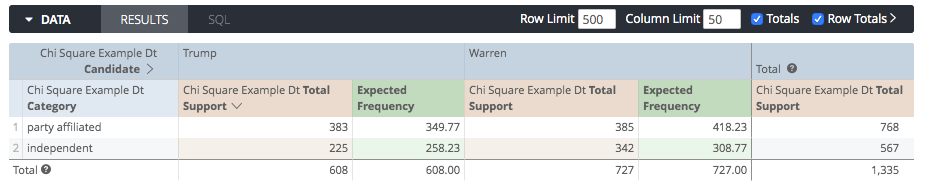
Step 3: Calculate the probability (or p-value):
Now that we have our actuals and expected values, we can now calculate the p-value.
We’ll create a second table calc named Chi-Square P-Value which will use the chisq_test function. The description of the function is:
“Returns the probability for the chi-squared test for independence between actual and expected data. actual can be a column or a column of lists, and expected must be the same type.”.
Since we’re dealing with a 2x2 Contingency, we’ll nest the pivot_row function within the chisq_test function a first time to return a list of the values of each candidate’s actual values, and a second time to return a list of the values of each candidate’s expected values:
chisq_test(
pivot_row(${chi_square_example_dt.total_support}),
pivot_row(${expected_frequency})
)
We now get this output:
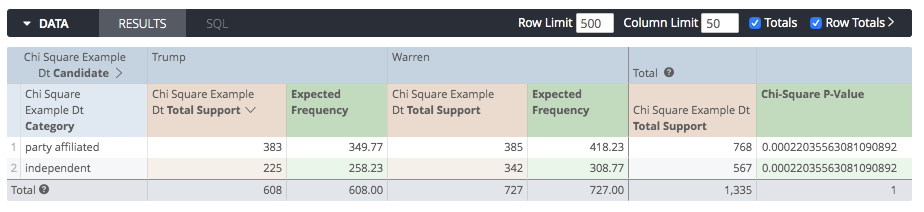
Step 4: Calculate the Chi-Squared (or χ2 )
Now that we have our p-value, we can calculate the Chi-Squared by using the chisq_inv function. The description states:
“Returns the position of probability on the inverse cumulative gamma distribution with dof degrees of freedom” .
For this function, we need to know the degrees of freedom. The formula for this is pretty simple as
dof = (number of rows - 1) * (number of columns - 1)
So (2-1) * (2-1) = 1. We’ll create a third table calc named Chi-Squared with the following expression:
chisq_inv(1-${chi_square_p_value}, 1)
Note: We’re substracting the p-value from 1 since the p-value measures the “tail” and the inverse function measures the “head”.
We now get this as an output:
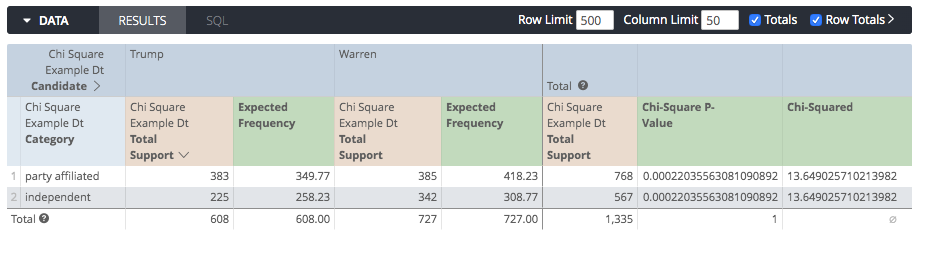
So there you go! The same principle would apply here for a bigger contingency table.
Step 5: Phi Coefficient
Let’s add the Phi Coefficient now. The formula is once again pretty simple:
√ (Chi-Squared / grand total).
Let’s create a table calc named Phi Coefficient with the following expression:
sqrt(${chi_squared}/sum(pivot_row(${chi_square_example_dt.total_support:total})))
Our output is now:

Step 6: Percentage of Voters
Let’s add a final, easy calculation to help us write our conclusion: let’s add the percentage of voters for each category. The expression for this additional table calc formatted as Percent (1) would be:
${chi_square_example_dt.total_support} / sum(${chi_square_example_dt.total_support})
Which gives us our final output:
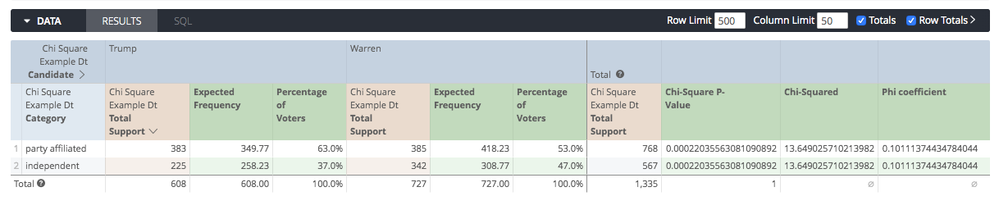
There you go! We now have all the numbers we need to write the conclusion:
A chi-square test was used to determine whether there was a significant
difference between the proportion of Warren and Trump’s supporters who are independent. Results indicated that 47.0% of Warren’s supporters were independents, whereas 37.0% of Trumps supporters were independents. This difference was statistically significant, χ2(1) = 13.65, p <.001. The phi coefficient, φ = .10, suggested a small effect.
Credits
- I want to thank @fabio1 from the Customer Success team who helped figuring this out. You rock! 💖
- Jason T. Newsom PhD., Professor at Department of Psychology, Portland State University, who wrote the document from which the example is taken from.
- Labels:
-
tablecalcs
-
access grant
4 -
actionhub
9 -
Actions
14 -
Admin
4 -
alert
29 -
Analytics
2 -
Analytics Block
35 -
Analytics General
1 -
API
12 -
bar
10 -
bestpractice
4 -
BigQuery
8 -
blocks
1 -
boards
4 -
Bug
168 -
cache
2 -
case
2 -
chart
17 -
cohort
1 -
connection
5 -
connection database
1 -
content access
1 -
content-validator
2 -
count
6 -
custom dimension
9 -
custom field
19 -
custom measure
8 -
customdimension
9 -
Dashboards
753 -
Data
5 -
Data Sources
4 -
data tab
4 -
Database
5 -
datagroup
2 -
date-formatting
14 -
dates
18 -
derivedtable
1 -
develop
1 -
development
3 -
dimension
17 -
done
8 -
download
19 -
downloading
9 -
drill-down
1 -
drilling
30 -
dynamic
1 -
embed
10 -
Errors
13 -
etl
1 -
explore
84 -
Explores
134 -
extends
1 -
feature-requests
10 -
filed
3 -
filter
245 -
Filtering
118 -
folders
4 -
formatting
19 -
git
2 -
Google Data Studio
2 -
Google Sheets
2 -
googlesheets
7 -
graph
9 -
group by
6 -
html
12 -
i__looker
1 -
imported project
2 -
Integrations
4 -
javascript
2 -
join
2 -
json
3 -
label
4 -
line chart
17 -
link
5 -
links
3 -
liquid
22 -
Looker
6 -
Looker Studio Pro
47 -
LookerStudio
7 -
lookml
169 -
lookml dashboard
15 -
looks
188 -
manage projects
1 -
map
30 -
map_layer
5 -
Marketplace
4 -
measure
4 -
Memorystore for Memcached
1 -
merge
14 -
model
3 -
modeling
2 -
multiple select
1 -
ndt
1 -
parameter
11 -
pdf
8 -
pdt
8 -
performance
7 -
periodoverperiod
5 -
permission management
1 -
persistence
1 -
pivot
21 -
postgresql
1 -
python
2 -
pythonsdk
2 -
Query
3 -
quickstart
4 -
ReactJS
1 -
redshift
4 -
release
16 -
rendering
8 -
Reporting
10 -
schedule
51 -
schedule delivery
5 -
sdk
1 -
Security
4 -
sharing
2 -
singlevalue
16 -
snowflake
3 -
sql
24 -
SSO
1 -
stacked chart
10 -
system activity
5 -
table chart
16 -
tablecalcs
144 -
Tile
12 -
time
8 -
time zone
3 -
totals
13 -
Training
1 -
Ui
19 -
usage
4 -
user access management
3 -
user management
3 -
user-attributes
6 -
value_format
4 -
view
4 -
Views
4 -
visualizations
558 -
watch
1 -
webhook
2
- « Previous
- Next »

 Twitter
Twitter